Midterm review activity questions
Kinematics, inverse kinematics, 3D orientation and spatial representation, Jacobian, 3d forward kinematics
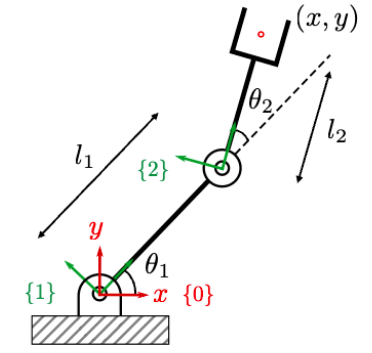
1. Forward kinematics. What is $x$ and $y$?
1. $$x = l_1 \cos\theta_1 + l_2 \cos\theta_2; \quad y = l_1 \sin\theta_1 + l_2 \sin\theta_2$$
2. $$x = l_1 \sin\theta_1 + l_2 \sin\theta_2; \quad y = l_1 \cos\theta_1 + l_2 \cos\theta_2$$
3. $$x = l_1 \cos\theta_1 + l_2 \cos(\theta_1 +\theta_2); \quad y = l_1 \sin\theta_1 + l_2 \sin(\theta_1+\theta_2)$$
4. $$x = l_1 \sin\theta_1 + l_2 \sin(\theta_1 +\theta_2); \quad y = l_1 \cos\theta_1 + l_2 \cos(\theta_1+\theta_2)$$
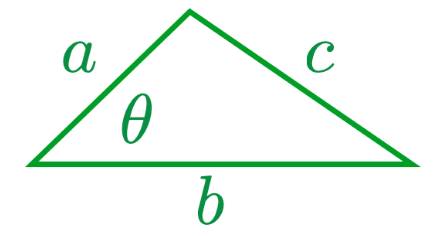
2. Cosine law. What is $c^2$?
1. $a^2 + b^2 - 2ab \sin\theta$
2. $a^2 + b^2 - 2ab \cos\theta$
3. $a^2 + b^2 + 2ab \sin\theta$
4. $a^2 + b^2 + 2ab \cos\theta$
3. Grubler's law. Select all correct statements of the following equation? $$m (N-1) - \sum_{i=1}^J (m - f_i).$$
1. $J$ is the number of links
2. $m$ is the dimension of the configuration space
3. $N$ is the number of links excluding the ground link
4. $f_i$ replies to the joint constraints
4. Jacobian. Select the option with all correct pairs.
1. Joint position → Cartesian position (Forward kinematics)
Joint position ← Cartesian position (Inverse kinematics)
Joint velocity → Cartesian velocity (Pseudo inverse jacobian)
Joint velocity ← Cartesian velocity (Jacobian)
2. Joint position → Cartesian position (Forward kinematics)
Joint position ← Cartesian position (Inverse kinematics)
Joint velocity → Cartesian velocity (Jacobian)
Joint velocity ← Cartesian velocity (Pseudo inverse jacobian)
3. Joint position → Cartesian position (Inverse kinematics)
Joint position ← Cartesian position (Forward kinematics)
Joint velocity → Cartesian velocity (Pseudo inverse jacobian)
Joint velocity ← Cartesian velocity (Jacobian)
4. Joint position → Cartesian position (Inverse kinematics)
Joint position ← Cartesian position (Forward kinematics)
Joint velocity → Cartesian velocity (Jacobian)
Joint velocity ← Cartesian velocity (Pseudo inverse jacobian)
5. S0(3). What is the $SO(3)$ for the rotation around the $z$-axis?
1. \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix}
2. \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix}
3. \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}
4. \begin{pmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}
6. so(3) to SO(3) What is the correct equation to transform $so(3)$ to $SO(3)$?
1. $$e^{[\hat{\omega}]\theta} = I + \sin\theta[\hat\omega] + (1-\cos\theta)[\hat\omega]^2$$
2. $$e^{[\hat\omega]\theta} = I + \sin\theta[\hat\omega] - (1+\cos\theta)[\hat\omega]^2$$
3. $$e^{[\hat\omega]\theta} = I - \sin\theta[\hat\omega] + (1-\cos\theta)[\hat\omega]^2$$
4. $$e^{[\hat\omega]\theta} = I + \sin\theta[\hat\omega] - (1-\cos\theta)[\hat\omega]^2$$
7. Quaternion. What is the dimension of the quaternion and what is the correct expression?
1. $$q \in \mathbb{R}^4, \quad \begin{pmatrix} \cos(\theta/2) \\ \hat\omega\sin(\theta/2) \end{pmatrix}$$
2. $$q \in \mathbb{R}^4, \quad \begin{pmatrix} \sin(\theta/2) \\ \hat\omega\cos(\theta/2) \end{pmatrix}$$
3. $$q \in \mathbb{R}^2, \quad \begin{pmatrix} \cos(\theta/2) \\ \hat\omega\sin(\theta/2) \end{pmatrix}$$
4. $$q \in \mathbb{R}^2, \quad \begin{pmatrix} \sin(\theta/2) \\ \hat\omega\cos(\theta/2) \end{pmatrix}$$
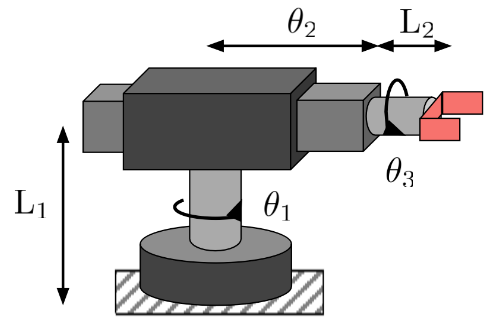
8. 3D Kinematics. Find the forward kinematkcs of a manipulator using $SE(3)$.
1. $${}_{0}T_3 = {}_{0}T_1 \, {}_{1}T_2 \, {}_{2}T_3 = \\ \begin{pmatrix} c\theta_1 & s\theta_1 & 0 & 0 \\ -s\theta_1 & c\theta_1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & \theta_2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & L_1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} c\theta_3 & -s\theta_3 & 0 & L_2 \\ s\theta_3 & c\theta_3 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$
2. $${}_{0}T_3 = {}_{0}T_1 \, {}_{1}T_2 \, {}_{2}T_3 = \\ \begin{pmatrix} c\theta_1 & -s\theta_1 & 0 & 0 \\ s\theta_1 & c\theta_1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & \theta_2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & L_1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} c\theta_3 & -s\theta_3 & 0 & L_2 \\ s\theta_3 & c\theta_3 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$
3. $${}_{0}T_3 = {}_{0}T_1 \, {}_{1}T_2 \, {}_{2}T_3 = \\ \begin{pmatrix} c\theta_1 & -s\theta_1 & 0 & 0 \\ s\theta_1 & c\theta_1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & \theta_2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & L_1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & L_2 \\ 0 & c\theta_3 & -s\theta_3 & 0 \\ 0 & s\theta_3 & c\theta_3 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$
4. $${}_{0}T_3 = {}_{0}T_1 \, {}_{1}T_2 \, {}_{2}T_3 = \\ \begin{pmatrix} c\theta_1 & s\theta_1 & 0 & 0 \\ -s\theta_1 & c\theta_1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & \theta_2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & L_1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & L_2 \\ 0 & c\theta_3 & s\theta_3 & 0 \\ 0 & -s\theta_3 & c\theta_3 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$
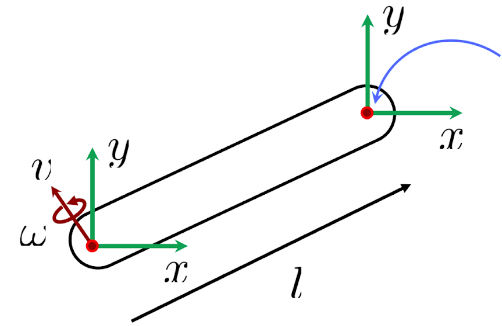
9. Velocity. What is the velocity of the point indicted with the blue arrow?
1. $$\begin{pmatrix} v \\ \omega l \end{pmatrix}$$
2. $$\begin{pmatrix} \omega \\ \omega + vl \end{pmatrix} $$
3. $$\begin{pmatrix} v \\ \omega + vl \end{pmatrix} $$
4. $$\begin{pmatrix} v \\ v + \omega l \end{pmatrix} $$
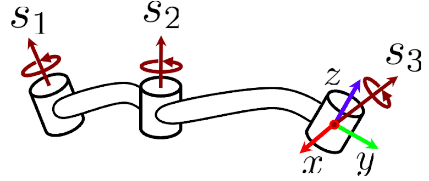
10. Generalized Velocity. What are the 6D velocity caused by $s_1$ and $s_2$? Assume $s_i$ is given as \begin{pmatrix}w_i\\v_i\end{pmatrix}
1. $$\begin{pmatrix} {}_{3}R_{1}\omega_1 \\ {}_{3}R_{1}\omega_1\times p_{1\rightarrow 3} + {}_{3}R_{1} v_1 \end{pmatrix} \\ \begin{pmatrix} {}_{3}R _{2}\omega_1 \\ {}_{3}R _{2}\omega_1\times p_{2\rightarrow 3} + {}_{3}R _{2} v_2 \end{pmatrix}$$
2. $$\begin{pmatrix} {}_{3}R _{1}\omega_1 \\ {}_{3}R _{1}\omega_1\times p_{1\rightarrow 3} + {}_{3}R _{1} v_1 \end{pmatrix} \\ \begin{pmatrix} {}_{3}R _{2}\omega_2 \\ {}_{3}R _{2}\omega_1\times p_{2\rightarrow 3} + {}_{3}R _{2} v_2 \end{pmatrix}$$
3. $$\begin{pmatrix} {}_{3}R _{1}\omega_1 \\ {}_{3}R _{1}\omega_1\times p_{1\rightarrow 3} + {}_{3}R _{1} v_1 \end{pmatrix} \\ \begin{pmatrix} {}_{3}R _{2}\omega_2 \\ {}_{3}R _{2}\omega_2\times p_{2\rightarrow 3} + {}_{3}R _{2} v_2 \end{pmatrix}$$
4. $$\begin{pmatrix} {}_{3}R _{1}\omega_1 \\ {}_{3}R _{1}\omega_1\times p_{1\rightarrow 3} + {}_{3}R _{1} v_1 \end{pmatrix} \\ \begin{pmatrix} {}_{3}R _{2}\omega_1 \\ {}_{3}R _{2}\omega_1\times p_{2\rightarrow 3} + {}_{3}R _{2} v_1 \end{pmatrix}$$